Analysis & design of RC structures

Analysis & design of RC structures

Analysis & design of RC structures is one of the modes in graphical user environment of the program. It is possible to assign arbitrary properties of concrete and reinforcement that is useful for analyses of reconstruction. In this mode you can unite several elements of the same type into one structural element (STE) and arrange reinforcement along the whole length of this element. Drawing of beams and columns are presented after analysis and can be saved as DXF files.

Working stress design

This design concept is based on elastic theory, assuming a straight line stress distribution along the depth of the concrete. The actual loads or working loads acting on the structure are estimated and members are proportioned on the basis of certain allowable stresses in concrete and steel. The allowable stresses are fractions of the crushing strength of concrete (fc') and the yield strength (fy). Because of the differences in realism and reliability over the past several decades, the strength design method has displaced the older stress design method

Limit state design

It is a further step in the strength design method. It indicates the state of the member in which it ceases to meet the service requirements, such as, loosing its ability to withstand external loads or local damage. According to limit state design, reinforced concrete members have to be analyzed with regard to three limit states:

1. Load carrying capacity (involves safety, stability and durability)
2. Deformation (deflection, vibrations, and impact)
3. The formation of cracks

The aim of this analysis is to ensure that no limiting sate will appear in the structural member during its service life.

Dead Loads:

Dead loads are those that are constant in magnitude and fixed in location throughout the lifetime of the structure. It includes the weight of the structure and any permanent material placed on the structure, such as roofing, tiles, walls etc. They can be determined with a high degree of accuracy from the dimensions of the elements and the unit weight of the material.

Live loads:

Live loads are those that may vary in magnitude and may also change in location. Live loads consists chiefly occupancy loads in buildings and traffic loads in bridges. Live loads at any given time are uncertain, both in magnitude and distribution.

Environmental loads:

Consists mainly of snow loads, wind pressure and suction, earthquake loads (i.e inertial forces) caused by earthquake motions. Soil pressure on subsurface portion of structures, loads from possible ponding of rainwater on flat surfaces and forces caused by temperature differences. Like live loads, environmental loads at any given time are uncertain both in magnitude and distribution.

Strucural Concrete elements

---

Slab:

Slabs are horizontal slab elements in building floors and roof. They may carry gravity loads as well as lateral loads. The depth of the slab is usually very small relatively to its length and width.

Beams:

Long horizontal or inclined members with limited width and height are called beams. Their main function is to transfer loads from the slab to the columns.

Column:

Columns are vertical members that support loads from the beam or slabs. They may be subjected to axial loads or moments.

Frames:

Frames are structural members that consists of combination of slab, beams and columns

Footings:

Footings are pads or strips that support columns and spread their load directly to the soil.

Walls:

Walls are vertical plate elements resisting gravity as well as lateral loads e.g retaining walls, basement walls. etc

Maximum reinforcement ratios for singly reinforced beams

---

ACI code limits the amount of reinforcement in terms of a minimum net tensile strain of 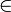= 0.005

Frther the ACI code defines a tension controlled member as one with a net tensile strain greater than or equal to 0.005. The coresponding strength reduction factor is Ø = 0.9. For compression controlled members as having a net tensile strain of less than 0.002. The strength reduction factor for compression controlled members is 0.65. A value of 0.70 may be used if members are spirally reinforced and ACI code allows a linear interpolation of Ø based on 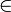as shown.

0.005 => Ø = 0.9

0.002 ==> Ø = 0.65

Graph of Net tensile strain

Minimum reinforcement ratio (ρmin)

---

If the external moment applied on the beam is very small and the dimensions of sections are specified (as is sometimes required architecturally) and are large than needed to resist the external ultimate moment, the calculations may show that very small or no steel reinforcement is required. In this case the maximum tensile stress due to bending moment may be equal to or less than the modulus of rupture of concrete.

If no rinforcement is provided, sudden failure will be expected when the first crack occurs, thus giving no warning. ACI code specifies a minimum steel area.

Design procedure for double reinforced beams

---

Step # 1:

Find the strength Mu of a singly reinforced beam /section using the already established 'b' and 'd' i.e. the dimensions of the section and with > ρ = ρ_max (OR) ρ for 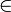= 0.005 to ensure that Ø = 0.90

M_u = Ø A_s f_y (d - a/2)

a = A_s f_y / 0.85 f_c' b

If M_u required > M_d of simply reinforced beam . Proceed with doubly reinforced beam design.

Step # 2:

Find excess moment i.e

M_u1 = M_u - M_u2

and determine the resulting compression steel area A_s1 = A_s and rentaively assume that f_s = f_y, then

A_s' = M_u1 /Ø f_y (d - d' )

Step# 3:

Find the total tensile stel area i.e

A_s = A_s' + A_s2

Step # 4:

Check whether the compression steel is yielding or not and use the corresponding stress in the steel for calculating the forces and moments. If compression steel is less than f_y, then the compression steel area is to be revised ==> A_s' f_s' < A_s' f_y ==> increase As rev.

The revised compression steel area acting at f_s must provide the same force as the trial steel area that was assumed to act at f_y.

So

C = T1

A'_{s rev} f '_s= A_{s trial} f_y

A'_{s rev} = A_{s trial} f_y / f_s'

Tensile steel area need not to be revised because it acts at f_y, as assumed.

Step # 5:

Check for satisfactory minimum and maximum reinforcement ratios

Step # 6:

Select appropriate bar size and draw the sketches.